Problemset 01

Prepared by Chams Eddine Abdelali Derreche

Problem 1

Alice and Kheira play the following game: starting with the number written on a blackboard, each player in turn changes the current number to a number , where is a prime divisor of . Alice goes first and the players alternate in turn. The game is lost by the one who is forced to write a number greater than .

Assuming perfect play, who will win the game?

Problem 2

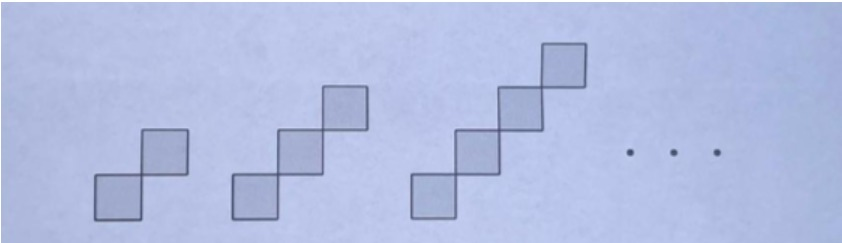
Omar has an board and wants to fill it with pieces composed of two or more diagonally connected squares as shown, without overlapping or leaving gaps:

1. Find all values of for which it is possible to fill the board.

2. If it is possible to fill an board, find the minimum number of pieces Omar can use to fill it.

Note: The pieces can be rotated.

Problem 3

Several positive integers are written in a row. Iteratively, Elyas chooses two adjacent numbers and such that and is to the left of , and replaces the pair by either or . Prove that he can perform only finitely many such iterations.

Problem 4

Let be an positive integer. Find the smallest integer with the following property; Given any real numbers $a_1 , \cdots , a_d $ such that and for , it is possible to partition these numbers into groups (some of which may be empty) such that the sum of the numbers in each group is at most .

Problem 5

Redhouane and Kheira play a game. At the beginning, Redhouane writes down a positive integer on the board. Then the players take moves in turn, Kheira moves first. On any move of his, Kheira replaces the number on the blackboard with a number of the form , where is a positive integer. On any move of hers, Redhouane replaces the number on the blackboard with a number of the form , where is a positive integer. Kheira wins if the number on the board becomes zero.

Can Redhouane prevent Kheira’s win?