Gift

Written by Raouf Ould Ali.

Problem Statement

• English
• French
• Arabic

We are given an array of size and an integer .

We start with and want to transform it into using operations of the form:

• Choose any integer
• Choose exactly distinct positions
• Add to all

The task is to either produce a valid sequence of operations with , or decide that it is impossible.

---

Step 1: Feasibility Conditions

Each operation increases the total sum of $B$ by $X \cdot K$.

• Thus,

  must be divisible by $K$.

• Let

  be the required “height” of each group.

• If $\max(A[i]) > \text{lim}$, then one element cannot fit into a single group, so the answer is impossible.

So feasibility requires:

---

Step 2: Grid Interpretation

Visualize a grid of size :

• The grid has height and width .
• Each column corresponds to one bundle of size .
• We place each vertically:
  • If it fits in the current column, it stays there.
  • If it overflows, it continues at the top of the next column.

Since for all , a box never skips a column. At most it is split into two consecutive columns.

---

Step 3: Sweeping for Operations

Instead of outputting one operation per row (which could be up to rows), we notice that:

• Each column contains one index at a time.
• The index for a column only changes when one ends and another begins.

Thus, while sweeping from bottom to top:

• We keep track of the current set of active indices for all columns.
• We only output an operation when this set changes.
• The operation covers all rows since the last change, so its increment is the height difference .

---

Step 4: Bound on Operations

• Each can start once in a column and possibly wrap once into the next column.
• Therefore, each contributes at most two changes.
• This means the total number of operations is at most , not .

This compression is what makes the solution efficient and ensures .

---

Step 5: Correctness Argument

1. Sum condition ensures the total number of increments matches.
2. Max condition ensures no element overflows beyond a single column boundary.
3. Because , there is no overlap in rows:
   • Every cell of the grid is covered by exactly one index.
4. The sweep construction outputs exactly the increments needed to reach , with no waste.

Therefore, the algorithm always finds a valid solution if and only if it exists.

---

Example

Input:

4 2
2 3 3 2

• , .
• Fill the grid column by column:

Column 1: [1, 1, 2, 2, 2]
Column 2: [3, 3, 3, 4, 4]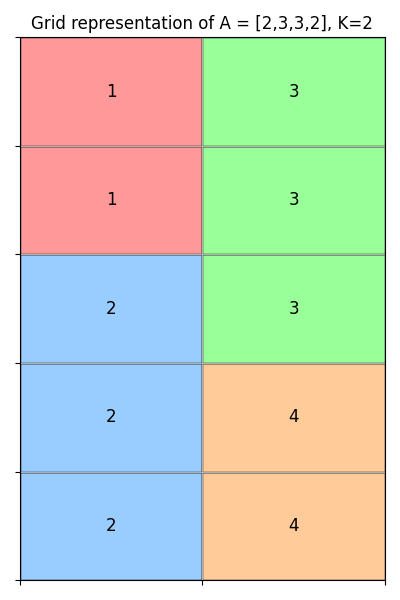

• Sweep rows:

  • Rows 1–2: active {1,3} → operation (2, 1 3)
  • Row 3: active {2,3} → operation (1, 2 3)
  • Rows 4–5: active {2,4} → operation (2, 2 4)

Output:

3
2 1 3
1 2 3
2 2 4

Implementation

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    ll n, k;
    cin >> n >> k;

    vector<ll> a(n);
    for (int i = 0; i < n; i++)
        cin >> a[i];
    ll sum = 0;
    ll max_ai = 0;
    for (int i = 0; i < n; i++) {
        sum += a[i];
        max_ai = max(max_ai, a[i]);
    }
    
    if(sum%k != 0 or max_ai > sum/k){
        cout << "-1\n";
        return 0;
    }

    ll max_height = sum/k;
    ll current_height = 0LL;
    ll current_column = 0LL;

    vector<vector<ll>> result;
    vector<tuple<ll, ll, ll>> cache; // height, column, index
    for (int i = 0; i < n; i++){
        cache.push_back({current_height, current_column, i+1});
        current_height += a[i];
        if(current_height >= max_height){
            current_height -= max_height;
            current_column += 1;
            if(current_column < k)
                cache.push_back({0, current_column, i+1});
        }
    }

    cache.push_back({max_height, 0, 0});

    sort(cache.begin(), cache.end());

    current_height = 0LL;
    vector<ll> current_move(k+1, 0);

    for(auto &[height, column, index] : cache){
        if(height != current_height){
            current_move[0] = height - current_height;
            result.push_back(vector<ll>(current_move.begin(), current_move.end()));
            current_height = height;
        }

        current_move[column+1] = index;
    }

    cout << result.size() << '\n';
    for(auto &x : result)
    {
        for(auto y : x) cout << y << ' ';
        cout << '\n';
    }
}